공부 125일차: 백준 15990번 1, 2, 3 더하기 5 자바 java

15990 1,2,3 더하기 5

https://www.acmicpc.net/problem/15990

15990번: 1, 2, 3 더하기 5

 

 

 

 

---

백준 15990번 문제 1, 2, 3 더하기 5

---

문제

---

 

 

 

---

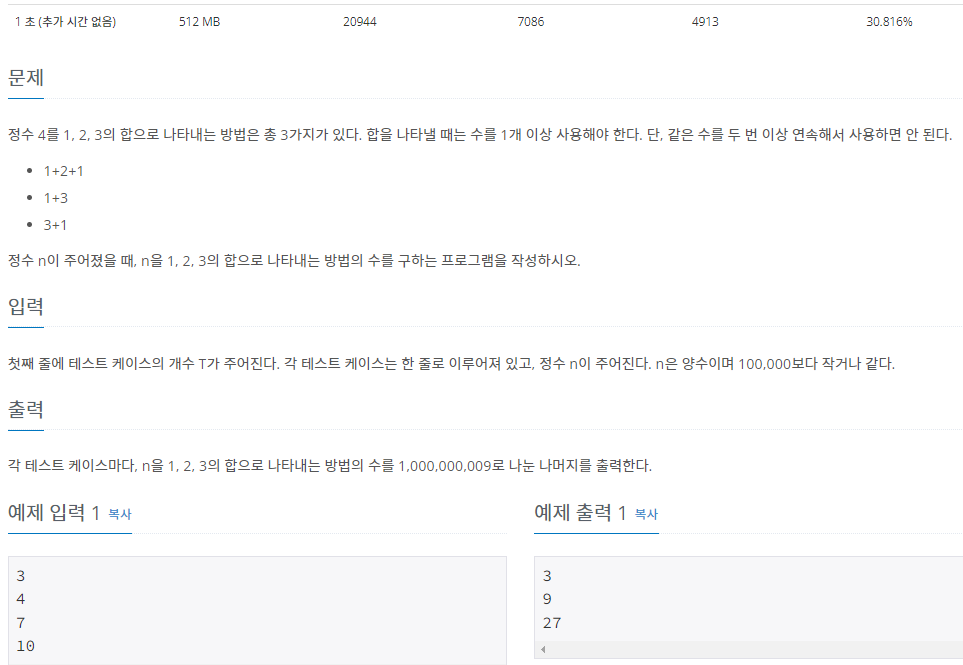
과정 생각해보기

---

 

https://gimbalja.tistory.com/205

공부 119일차: 백준 9095번 1, 2, 3 더하기 자바 java

이 문제와 비슷한 듯 보이지만 나는 많이 다르다고 생각한다

 

차례대로 그려보면서, 1, 2, 3으로 끝나지 않는 수에 반대되는 1, 2, 3을 더하는 것까진 알아냈는데

이걸 어떻게 알고리즘으로 구현해야 하는지 몰랐다

 

 

https://pangtrue.tistory.com/317

이 블로그를 보니 그 끝자리에 따라 다르게 주기 위해, 2차원 배열을 선언하면 되는 거였다

 

 

 

 

---

정답 인정 코드

---

 

import java.io.*;
 
public class Main {
 
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        
        int t = Integer.parseInt(br.readLine());
        final int N = 1_000_000_009;
        
        long[][] dp = new long[100_001][4];
        dp[1][1] = 1;    //1일 때 1로 끝나는 개수 (1)
        dp[2][2] = 1;    //2일 때 2로 끝나는 개수 (1)
        dp[3][1] = 1;    //3일 때 1로 끝나는 개수 (2+1)
        dp[3][2] = 1;    //3일 때 2로 끝나는 개수 (1+2)
        dp[3][3] = 1;    //3일 때 3로 끝나는 개수 (3)
        
        for(int i = 4; i < 100_001; i++) {
            dp[i][1] = (dp[i-1][2] + dp[i-1][3])%N;
            dp[i][2] = (dp[i-2][1] + dp[i-2][3])%N;
            dp[i][3] = (dp[i-3][1] + dp[i-3][2])%N;
        }
        
        
        for(int i = 0; i < t; i++) {
            int n = Integer.parseInt(br.readLine());
            System.out.println((dp[n][1]+dp[n][2]+dp[n][3])%N);
        }
 
    }
 
}

 

주의할 점이라면 long 타입으로 선언한다는 점, 또다시 오버플로우를 막기 위해 1,000,000,009의 나머지로 구한다는 점이겠다

 

 

---

 

다 구했는데도 방법을 생각 못해낸 게 너무 아쉽다

그 전 문제랑 똑같은 패턴일 거라는 생각에 너무 매몰되어 있었던 것 같다

풀이 하나만 정답일 리가 없다는 걸 상기하기