공부 140일차: 백준 11055번 가장 큰 증가 부분 수열 자바 java

11055 가장 큰 증가 부분 수열

https://www.acmicpc.net/problem/11055

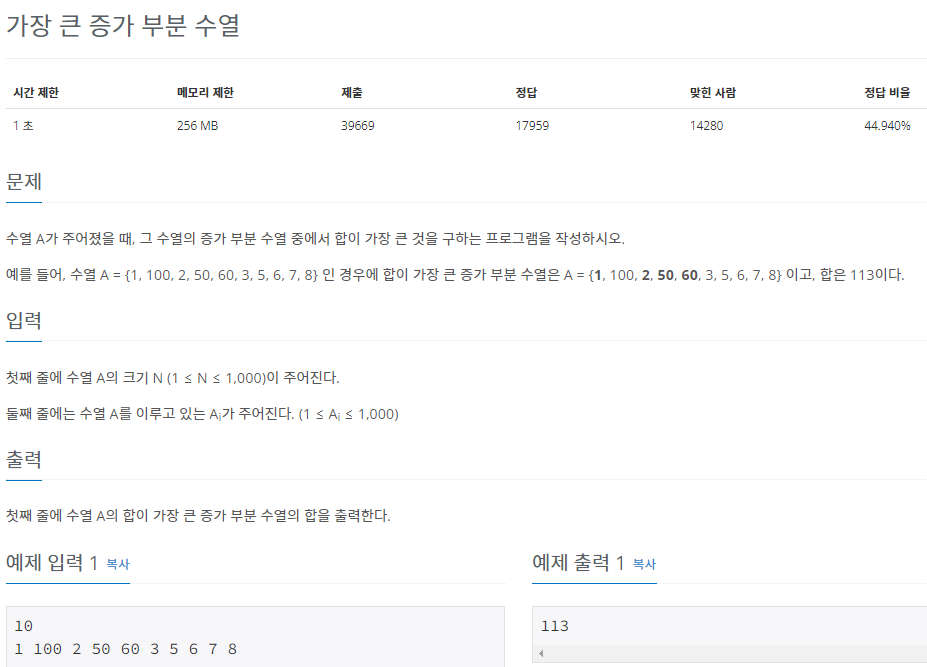
11055번: 가장 큰 증가 부분 수열

 

 

 

 

---

백준 11055번 문제 가장 큰 증가 부분 수열

---

문제

---

 

 

 

 

---

과정 생각해보기 & 오답

---

 

https://gimbalja.tistory.com/249

공부 128일차: 백준 11053번 가장 긴 증가하는 부분 수열 자바 java

https://gimbalja.tistory.com/250

공부 129일차: 백준 14002번 가장 긴 증가하는 부분 수열 4 자바 java

 

비슷한 문제는 위의 두 링크다

다만 dp[]를 수열의 길이로 두었던 두 문제와 다르게, dp[]에 수열의 합을 저장한다는 것이 다른 점이다

 

수열의 합을 저장하게 되는 원리는 다음과 같다

10
1 100 2 50 60 3 5 6 7 8

예제처럼 이런 배열이 주어질 때

 

dp[0] = 1

dp[1] = 100 (자기자신) / 101(수열이라면 이전 수열에서의 dp값에 자신을 더한다: 1 + 100)

dp[2] = 2 / 3(자신의 이전 수열에서의 dp값에 자신을 더한다: 1 + 2) 

dp[3] = 50 / 53(3 + 50)

dp[4] = 60 / 113(53 + 60)

dp[5] = 3 / 6(3(이전 수열인 dp[2]) + 3)

...

 

이때 자신의 이전 수열인지는 그전에 자기 자신보다 작은 값인지 확인하면 된다

그렇게 구한 최종 점화식은

(arr[j]가 arr[i] 보다 작을 때, 즉 arr[j], arr[i]가 수열을 이룰 때)

dp[i] = Math.max(dp[i], dp[j]+arr[i]);

 

밑에 조금 잘리긴 했지만, 문제의 예시에서는 이런 과정을 거치게 된다

 

이후 dp[]들 중에서 가장 큰 값을 출력하면 된다

 

 

 

---

정답 인정 코드

---

 

import java.io.*;
import java.util.*;
 
public class Main {
    
    static int[] arr;
    static int[] dp;
 
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = null;
        
        int n = Integer.parseInt(br.readLine());
        arr = new int[n];
        dp = new int[n];
        
        st = new StringTokenizer(br.readLine());
        for(int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
            dp[i] = arr[i];
        }
        // 디버깅 System.out.println(Arrays.toString(arr));
        
        for(int i = 1; i < n; i++) {
            for(int j = 0; j < i; j++) {
                if(arr[j] < arr[i]) {
                    dp[i] = Math.max(dp[i], dp[j]+arr[i]);
                    //System.out.println(dp[i]);
                }
            }
        }
        
        int max = 0; // 수열은 1부터 시작하므로
        for(int i = 0; i < n; i++) {
            max = Math.max(max, dp[i]);
        }
        System.out.println(max);
 
    }
}
 

 

까다로워 보이긴 하지만, 결국 LIS를 구했을 때, 자신보다 작은 수면 그 수까지의 길이에 1을 더했듯이

이전에 작은 수가 존재했다면 그 수까지의 합에 자신을 더하면 되는 것이다

 

 

 

---

dp문제는 점화식을 구하는 과정이 엄청 재밌지만, 글로 설명하는 게 어렵다