공부 143일차: 백준 13398번 연속합 2 자바 java

133398 연속합 2

 

https://www.acmicpc.net/problem/13398

13398번: 연속합 2

 

 

 

---

백준 13398번 문제 연속합 2

---

문제

---

 

 

 

---

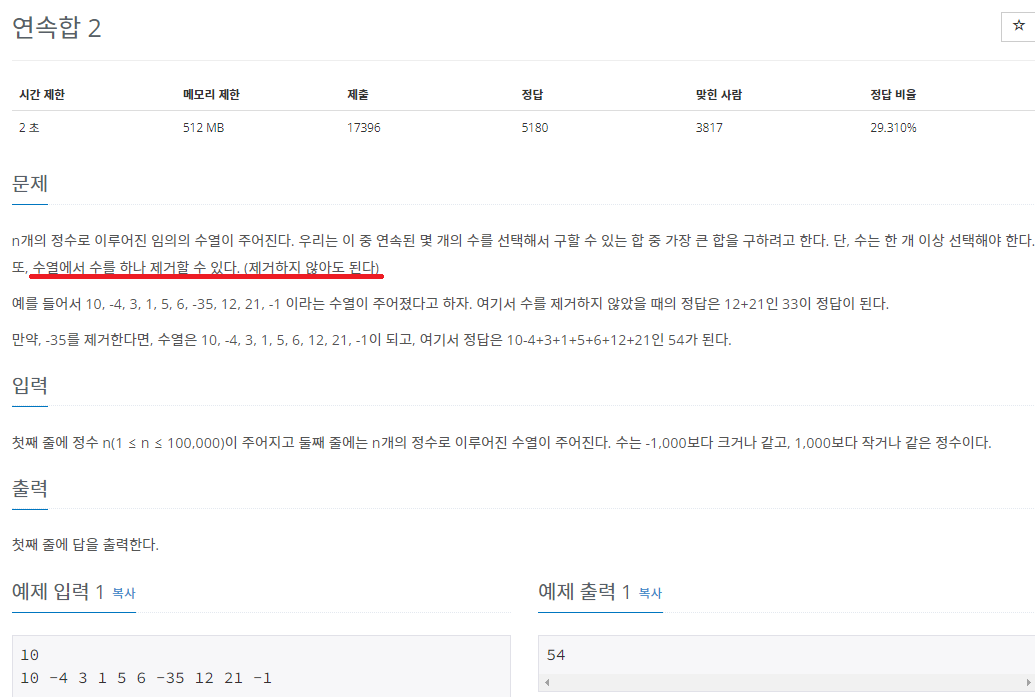
과정 생각해보기 & 오답

---

 

https://gimbalja.tistory.com/251

공부 130일차: 백준 1912번 연속합 자바 java

위와 유사한 문제

수열에서 수를 하나 제거할 수 있느냐 없느냐가 다른 점이다

 

 

import java.io.*;
import java.util.*;
 
public class Main {
 
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = null;
        
        int n = Integer.parseInt(br.readLine());
        
        int[] arr = new int[n];
        int[] dp = new int[n];
        int[] sum = new int[n];
        
        st = new StringTokenizer(br.readLine());
        for(int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
            dp[i] = arr[i];
        }
        
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < i+1; j++) {
                sum[i] += arr[j];    // sum[i]는 arr[0]~arr[i]까지의 누적합
            }
            //System.out.println(sum[i]);
        }
        
        // 원래 연속합
        for(int i = 1; i < n; i++) {
            dp[i] = Math.max(dp[i], dp[i-1]+arr[i]);
        }
        
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < i; j++) {
                // 누적합에서 중간수를 빼면 그 숫자를 삭제한 것과 같다
                dp[i] = Math.max(dp[i], sum[i]-arr[j]);
            }
        }
        
        Arrays.sort(dp);
        System.out.println(dp[n-1]);
    }
 
}
 

 

예시로 주어진 수열은 정답과 같았지만, 채점은 오답으로 받은 코드다

기존처럼 연속합을 구한 뒤, i까지의 누적합에서 하나씩 빼보면서 가장 큰 수를 찾는 코드인데,

sum[i]가 무조건 처음부터 i번까지의 합을 가지므로 이게 매번 최대값일 리 없으므로 문제가 원하는 방식이 아니다

 

결국 오래 고민해보아도 방법이 떠오르지 않아

https://steady-coding.tistory.com/181

이 블로그를 참고했다

 

두 가지 방법을 소개하고 있는데, 이 중 왼쪽/오른쪽으로 나누어 구하는 방법이 재미있어 보였다

(다른 블로그들이 다 2차원 배열만 있기도 하고)

원리를 그림으로 표현하면 위와 같다

i를 제외한 연속합은 dpR[i-1] + dpL[i+1]가 되는 것이다

 

 

 

---

정답 인정 코드

---

 

import java.io.*;
import java.util.*;
 
public class Main {
 
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = null;
        
        int n = Integer.parseInt(br.readLine());
        
        int[] arr = new int[n];
        int[] dpR = new int[n];
        int[] dpL = new int[n];
        
        st = new StringTokenizer(br.readLine());
        for(int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
            dpR[i] = dpL[i] = arr[i];
        }
        
        // 오른쪽 방향으로 최대 연속합 저장 (기존 연속합과 동일)
        int max = dpR[0];
        for(int i = 1; i < n; i++) {
            dpR[i] = Math.max(dpR[i], dpR[i-1]+arr[i]);
            max = Math.max(max, dpR[i]);    // 기존 연속합 최대값 구하기
        }
        // 왼쪽 방향으로 최대 연속합 저장
        for(int i = n-2; i >= 0; i--) {
            dpL[i] = Math.max(dpL[i], dpL[i+1]+arr[i]);
        }
        
        // 숫자를 아무것도 지우지 않았을 때(원래 연속합)랑 무언가를 지웠을 때 중 큰 값 산출
        for(int i = 1; i < n-1; i++) {
            int exceptI = dpR[i-1]+dpL[i+1];
            // arr[i]를 뺀 값 : dpR[i-1]+dpL[i+1] (i 전까지의 최대값 + i 후의 최대값)
            
            max = Math.max(max, exceptI);
        }
        System.out.println(max);
    }
 
}

 

접근법이 새로워서 재밌었다

 

 

 

 

---

혼자 못 풀어서 아쉽다

골드 문제는 어렵구만